Pytorch学习

Pytorch学习

[toc]

基本操作

查看package的相关内容函数

• dir()：解包，显示库内所含的内容，显示内容为下划线开始的命名时，说明该内容为函数，可以使用
• help()：可以显示该函数的使用方法和类型

上述两幅图片分别是使用下两行代码运行的结果，其中help()要把函数的括号去掉

import torch
print(dir(torch,cuda))
print(help(torch.cuda.is_available))

注：在jupyter notebook中，shift+enter能够执行代码段，包名加??可以显示具体内容

检测pytorch是否可运行GPU加速

import torch

print(torch.cuda.device_count())
print(torch.cuda.get_device_name(0))
print(torch.cuda.is_available())

torch.stack((x,y),dim=0)：可以将x和y增加维度的合并

torch.cat((x,y),dim=0)：可以将x和y不增加维度合并

基本运算

pytorch与numpy之间数组的转换：torch.from_numpy()

定义张量：torch.Tensor([3,4])

定义浮点张量：torch.FloatTensor([3,4])

定义随机维度张量矩阵：torch.randn(3,4)

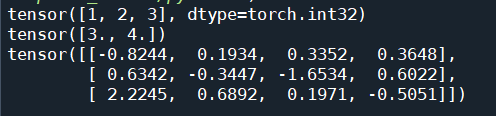
相关结果如上

经过测试，tensor的访问与列表操作一直，也支持切片等操作

tensor与numpy之间的相互转换

np_tensor=np.random.randn(3,4)
print(np_tensor)
py_tensor=torch.from_numpy(np_tensor)
print(py_tensor)
new_np_tensor=py_tensor.numpy()
print(new_np_tensor)

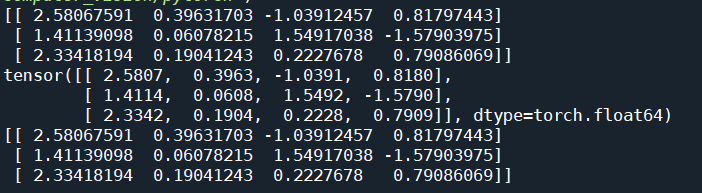
GPU tensor与CPU tensor相互转换

x=torch.randn(4,4)
x_gpu=x.cuda(0) # 将x放在第一块GPU上进行运算
print(x_gpu)
x_cpu=x_gpu.cpu() # 将GPU的资源放到CPU上运算
print(x_cpu)

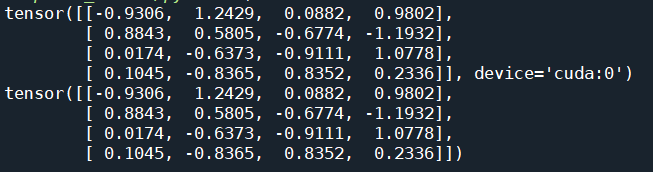
注意：只用CPU上的资源可以转换为numpy，直接将GPU转化为numpy会报错，因此需

x_array=x_gpu.cpu().numpy()

Tensor操作

数学运算

x=torch.ones(3,4)
y=torch.ones(3,4)
z=torch.ones(4,3)
k=x+3             # 矩阵与标量运算
k=torch.add(x,3)  # 矩阵与矩阵运算
k=torch.mm(x,z)   # 矩阵与矩阵的乘法(叉乘),(1,2)*(2,3)=(1,3)
k=torch.mul(x,y)  # 矩阵与矩阵的点乘,(1,2).(1,2)=(1,2)

高级运算

x=torch.randn(4,3)
print(x.size())
print(x.shape)    # 注意shape不带括号

重新排列矩阵

x=x.view(3,4)，x=x.view(12)

将上述生成4*3矩阵转换成3*4以及12维行向量

增加维度

torch.unsqueeze(x,dim=1)

torch.unsqueeze(x,dim=1)
x=x.unsqueeze(1)
x.shape

此时输出结果为torch.Size([4,1,3])

若要减少维度可以使用torch.squeeze(x,dim=1)

查询最大最小值

print(x)
max_value,max_index=torch.max(x,dim=1)
print(max_value,max_index)
# 也可写成
max_value,max_index=x.max(1)

注意，torch.max(x,dim=1)函数，返回每一行的最大值与索引，先是值，后索引。并且0代表列，1代表行

x.sum(0)：输出每一列的和

Variable操作

from torch.autograd import Variable
x=Variable(torch.ones(2,2),
           requires_grad=True)
y=Variable(torch.ones(2,2),
          requires_grad=True)
z=torch.sum(x+y)
print(z.data)
z.backward()
print(x.grad)

requires_grad参数表示是否需要对这个参数进行求导，对其使用z.backward()后，通过x.grad可访问具体值

x=Variable(torch.FloatTensor([2]),requires_grad=True)# []不可省略
z=(x+2)**2
z.backward()
print(x.grad)
print(z.data)

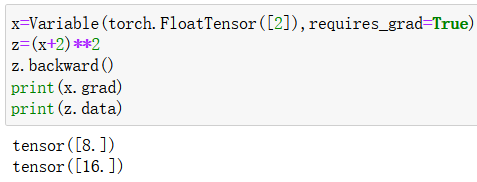
第一行表示该函数导数在x=2的值，第二行表示该函数在x=2的值

神经网络

线性模型

时间	成绩
2	3
3	5
4	8
5	?

$$
\hat{y_i}=wx_i+b
$$

其中$\hat{y_i}$表示预测的结果，$y_i$表示真实的结果，误差即为
$$
\frac{1}{n}\sum^n_{i=1}(\hat{y_i}-y)^2
$$
模型通过该loss，修改$wi$和$b$的值，使得loss越接近于零，引入梯度下降概念

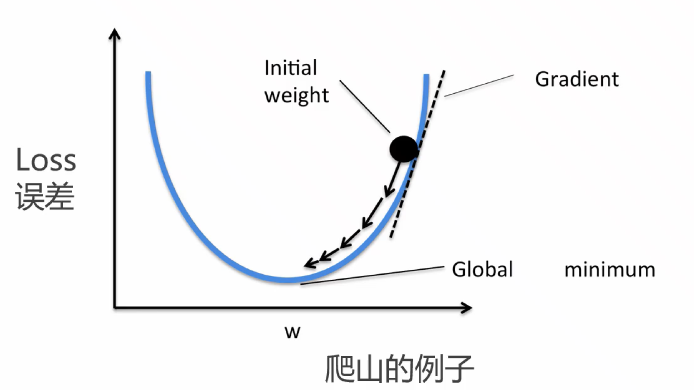
$$
w=w-\eta\frac{\delta loss}{\delta w}
$$
$\eta$即为学习率，通过代码显示即为：

def liner_model(x):
    return w*x+b
def get_loss(y_,y):
    return torch.mean((y_-y)**2)

w=Variable(torch.randn(1),requires_grad=True)
b=Variable(torch.randn(1),requires_grad=True)
x_train=torch.FloatTensor([1,2,3,4,5,6,7,8])
y_train=torch.FloatTensor([5.1,5.95,7.2,8.02,8.99,10.05,11.15,12.03])

for e in range(10):
    y_=liner_model(x_train)
    loss=get_loss(y_,y_train)
    

    loss.backward()

    w.data=w.data-1e-2*w.grad.data
    b.data=b.data-1e-2*b.grad.data
    #保险起见推荐用下表述，上述表述新起了一个变量暂存w，可能会丢失Variable的属性，但实测高版本无影响
    #w.data-=1e-2*w.grad.data
    #b.data-=1e-1*b.grad.data
    w.grad.zero_()# 梯度归零
    b.grad.zero_()
    print(w.data,b.data)
print("w:",w.data,"b:",b.data,"predict:",9*w.data+b.data)

其中，每次迭代需要将梯度归零，这里经过查阅资料发现，需要将清零操作放置在梯度下降后，输出结果如下

假象解为w=1,b=4，经过实际测试发现，与随机初始的w,b值有关，以及跟学习率的大小也很相关（炼丹玄学）

Logistic回归模型

针对分类问题
$$
\hat{y_i}=\sigma(w_ix+b)
$$
其与线性回归唯一不同，多了个sigmoid函数，范围在0~1之间，常常处理二分类问题，因为其二值化的值域可以有效的进行二分类的区分（0到1的概率）
$$
\sigma(x)=\frac{1}{1+e^{-x}}
$$
其loss函数相较于线性模型更加的复杂
$$
loss=-\frac{1}{n}\sum^n_{i=1}(y_ilog\hat{y_i}+(1-y_i)log(1-\hat{y_i}))
$$
注意：在二分类问题中，$y_i$只有0和1两个取值，因为其真实结果是确定的

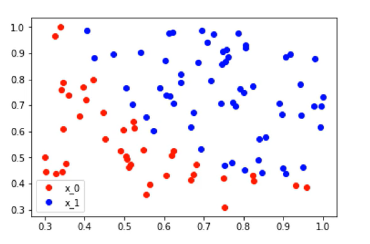
对于如该点图分布，使用逻辑斯蒂回归进行二分类

def sigmoid(x):
	return 1/(1+np.exp(-x))
# 或者直接使用pytorch内置的sigmod函数
import torch.nn.functional as F
F.sigmoid()
w=Variable(torch.randn(2,1),requires_grad=True)
b=Variable(torch.zeros(1),requires_grad=True)
def logistic_regression(x):
	return F.sigmoid(torch.mm(x,w)+b)
def binary_loss(y_pred,y):
    logits=(y*y_pred.clamp(1e-12).log()+(1-y)*(1-y_pred).clamp(1e-12).log()).mean()
    return logits

其中，该数学表达式可写成
$$
\hat{y}=\sigma(w_1x+w_2y+b)
$$
上述仅适合于少量参数情况下，如果参数上百个之多，便需要使用优化器来迭代梯度

from torch import nn
w=nn.Parameter(torch.randn(2,1))
b=nn.Parameter(torch.zeros(1))

def logistic_regression(x):
	return F.sigmoid(torch.mm(x,w)+b)

optimizer=torch.optim.SGD([w,b],lr=1.)
optimizer.zero_grad()#使用优化器将梯度归零
loss.backward()
optimizer.step()# 使用优化器来更新参数

多层神经网络

应对复杂问题，可以在输入和输出之间嵌套多个线性层和激活函数（即隐含层）。

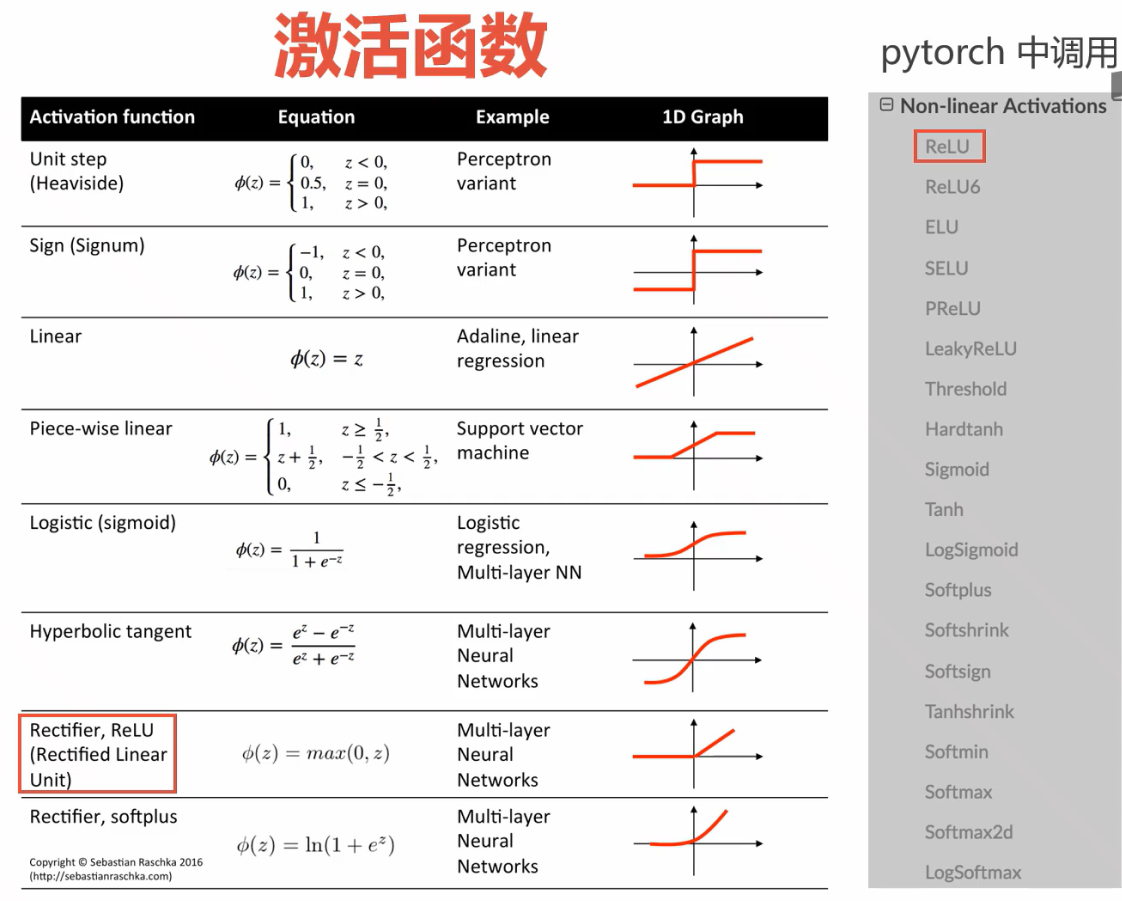
为什么加激活函数？

对于一个两层神经网络：
$$
y=w_2\sigma(w_1x)
$$
若不加激活函数$\sigma$，该网络将变成单一线性网络
$$
y=w_n\dots w_1x=\hat{w}x
$$

多层神经网络的写法

一般分为Sequential和Module两类，其中Module的写法更为灵活，因为Module可以使用Sequential

一些注意事项：

• sigmoid等等函数集成在了torch.sigmoid位置，老版本还在F中
• 套用变量时候需要Variable(torch.from_numpy(x).float())，时刻注意tensor和numpy的转换
• jupyter notebook似乎可以保存上次的参数继续训练
• 在一些浅层的tanh网络中，学习率可以稍微设大一点。
• 网络的设置把握好欠拟合和过拟合的度

seq_net = nn.Sequential(
    nn.Linear(2, 4), 
    nn.Tanh(),
    nn.Linear(4, 1)
)
print(seq_net[0])
w0=seq_net[0].weight
print(w0)
param=seq_net.parameters()
optim=torch.optim.SGD(param,5e-1)

for e in range(20000):
    out = seq_net(Variable(x))
    loss = criterion(out, Variable(y))
    optim.zero_grad()
    loss.backward()
    optim.step()
    if (e + 1) % 1000 == 0:
         print('epoch: {}, loss: {}'.format(e+1, loss.data))

上为Sequential()方式定义网络

下为Module类的方式定义网络

class module_net(nn.Module):
    def __init__(self,numb_perlayer):
        super(module_net,self).__init__()
        self.layer1=nn.Linear(numb_perlayer[0],numb_perlayer[1])
        self.layer2=nn.Tanh()
        self.layer3=nn.Linear(numb_perlayer[1],numb_perlayer[2])
        self.layer4=nn.Tanh()
        self.layer5=nn.Linear(numb_perlayer[2],numb_perlayer[3])
    def forward(self,x):
        x=self.layer1(x)
        x=self.layer2(x)
        x=self.layer3(x)
        x=self.layer4(x)
        x=self.layer5(x)
        return x
optim = torch.optim.SGD(mo_net.parameters(), 0.1)
for e in range(30000):
    out = mo_net(Variable(x))
    loss = criterion(out, Variable(y))
    optim.zero_grad()
    loss.backward()
    optim.step()
    if (e + 1) % 1000 == 0:
        print('epoch: {}, loss: {}'.format(e+1, loss.data))

同样也有两种保存训练好的模型的方式

• torch.save(seq_net,"save_seq_net.pth")：该方式会将网络的模型也保存下来
• torch.save(seq_net.state_dict()."save_seq_net_params.pth")：该方式仅保存参数而不保存模型结构

同样，调用时候，第一种直接torch.load("xxx.pth")，而第二种先完整定义网络，再导入参数seq_net2.load_state_dict(torch.load("xxx.pth"))

推荐在项目开头，设定随机种子进行使用

def setup_seed(seed):
    #random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)
    torch.backends.cudnn.benchmark = False
    torch.backends.cudnn.deterministic = True

setup_seed(123)def setup_seed(seed):
    #random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)
    torch.backends.cudnn.benchmark = False
    torch.backends.cudnn.deterministic = True

setup_seed(123)

多分类问题

网络仍为线性层，但是最后不使用sigmoid()函数，而是使用softmax函数进行多分类的概率匹配
$$
softmax(z_i)=\frac{e^{z_j}}{\sum^k_{j=1}e^{z_j}}
$$
同时，对于多分类下的Loss函数，我们也需要探求一般性计算公式以匹配任意多分类问题，即交叉熵
$$
CrossEntropy(p,q)=-\frac{1}{m}\sum_xp(x)log\space q(x)
$$
可以看出，二分类问题的loss也是该公式的变种

赏

谢谢你请我吃糖果

支付宝

微信

• 本文作者： Isabella
• 本文链接： https://username.github.io/2023/11/16/Pytorch学习/
• 版权声明： 本博客所有文章除特别声明外，均采用 MIT 许可协议。转载请注明出处！